
《应用数学学报》


在世界数学难题中,最著名的当属7个千禧问题了。这是一系列的问题,解决其中任何一个都可以获得100万美元。黎曼假设是最容易表述的,所以有很多关于它的文章。庞加莱猜想是迄今为止唯一一个被解决的,因此也有许多关于它的文章。
这篇文章将要讨论的问题叫做霍奇猜想(Hodge Conjecture)。这是一个代数几何的问题。本文尝试为一般的数学读者提供这个猜想的概述。
拓扑学基本上是研究如何使物体变形的。首先,我们设一个空间X是一个球面(二维的)。

如果我们从球面上的任何一个环(比如黑色的那个)开始,我们可以将它滑动到一个点(黑点)。当我们可以这样做的时候,我们把这个环称为“等于0”,因为这个环可以变为一个点。
对于这个球面上的任何一个环,我们都可以将它滑到一个点,所以这个变形等价的环的集合为0。我们用下式表示这种情况

需要注意的一件重要的事情是,开始的环并不一定是一个“平滑的循环”。它可以是任意的形状,只要它是一个闭环即可。下标1表示研究的环是一维的(在二维平面中)。
让我们增加一点难度,看看环面(也是二维的)。

上图中红色的环可以变形到环面上的一点。但是黑色的环(上图波状黑圈)则不能缩到一个点上,它最多可以变成上图光滑的黑圈。

任何环绕中心孔的闭环都可以缩小到中间的环上(上图红色圈)。严格地证明并不容易,因为我还没有给出真正的定义,但是如果你仔细想想,你应该能够说服自己,环面只有以上这三种情况。
所以,唯一的非零元素是由这两个环产生的。在本例中(环面),我们用下式表示:
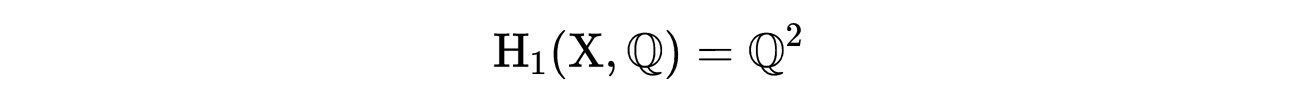
它是第一个同调群。如果一个环是[A],另一个环是[B],我们可以用有理数作为系数对它们求和,如:
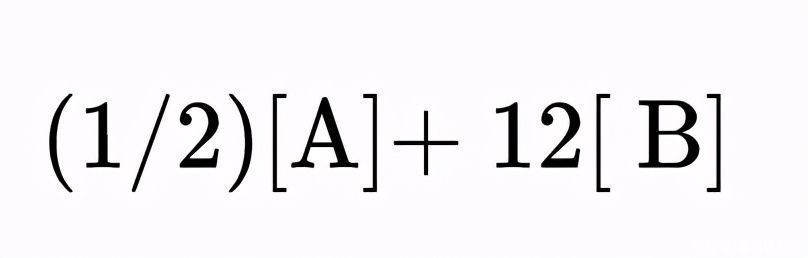
如果我们称这些一维的环为1环,那么我们就称k维的对应环为k-环。准确地定义它们有点奇怪,因为我们仍然希望在更高的维度中有“成为一个环”的概念。
为了感受一下,你可以想象一个3d球体:

如果你有一些二维的小块在里面,你总是可以把它缩小到一个点。从图上很难分辨,但你应该注意到这是在三维球体的内部。在之前的例子中,我们必须在二维球面上。
k-环的情况用下式表示:
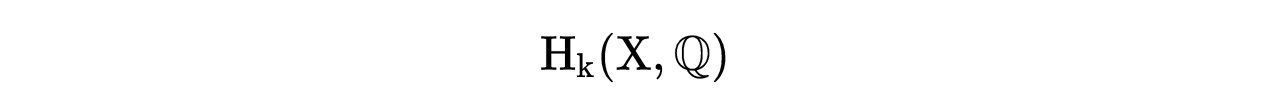
由于所有的1-环都会缩到球面上的一点,因此:
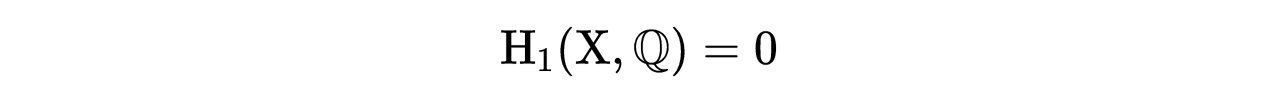
所有的2-环也会缩到一点,因此:
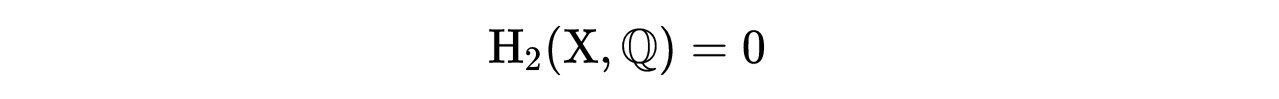
在某种意义上,H的维数k将告诉你在空间X中有多少个(n-k)维孔,其中n是X的维数。H_1是二维的,因为它有两个“孔”,一个绕着环面的“管”,另一个绕着中心孔。
几何可以表示很多不同的东西,但在本文中,我们用的是“代数几何”。如果你学过线性代数,你应该对这个概念很熟悉。线性代数研究的是线性方程组的零集。你会得到非常简单的东西,比如平面和子空间。
回想一下,线性代数中的技巧包括在思考“图像”(比如零空间、值域空间、平面的交点)和实际计算的“代数”之间来回转换。
线性代数在某种意义上是“完全解决了”,但如果你让你的方程中有不同指数,那它们就是多项式。这就是代数几何:在多项式零集的几何和处理这些方程的代数运算之间进行转换。
在本文中,一个光滑代数簇(简化为“簇”)是一个几何空间X,由多项式的零集给出,得到的空间是"光滑的",就像你们在微积分中学到的那样。
二维球面由二次方程给出。圆环面是由三次方程给出的椭圆曲线。希望你们理解了这个奇怪的术语。椭圆曲线是一个二维环面。
因为我们处理的是复数,所以“实”维数总是偶数。如果你考虑复平面,它看起来像:

但它只是?。代数几何学家用复维来称呼事物,所以一维曲线有2个实维,而二维曲面有4个实维。
上一篇:高考答题提分技巧 数学强化解题规范训练
下一篇:没有了