伊朗伊玛目清真寺中的几何密铺。（图片来源：Hosein Aghaei）

大家对瓷砖应该很熟悉，瓷砖多是三角形、四边形和六边形，很少有其他形状的。那么，能够铺满任意平面的瓷砖是不是只有这些形状呢？

这个问题自古希腊时代就吸引着数学家们。在数学中也有专门研究能够铺满整个平面而不留空隙的地砖图形的分支——密铺（tessellation）。被尊为伟大的数学家的戴维·希尔伯特 (David Hilbert)曾在1900年将密铺问题列为他的23个问题之一。

当然，除了贴瓷砖，密铺在日常生活中也有很重要的应用。比如，显卡大都是利用三角形的密铺性质实现渲染的。渲染的速度和效果严重影响了用户体验，爱打电脑游戏的人应该有一手的感悟。

在制造业，为了减少原材料的浪费（如切割车门所用的金属），在制作模型时也要尽可能使用密铺图形。

许多人不知道的是，一位只有高中学历的家庭妇女，却在天命之年为这个数学分支做出了重要的贡献，美国数学学会（MAA）甚至用她发现的密铺图形铺地砖。一起来看看这位传奇的女士的故事吧。

玛乔丽·赖斯（图片来源：Sharon Whittaker）

1923年，玛乔丽·赖斯（Marjorie Rice）出生在美国佛罗里达州的一个普通农户家庭里。在上中学时，她跳了两级。后来在高中时期，她选了文秘方向，只修了一门数学课，因为在当时，女孩子只能选一门数学课。

而由于时代对女性的限制以及家庭的贫困，她没有上大学。高中毕业后不久，她嫁人生子，成了一名家庭主妇。

时间推进到1975年。那时，已经52岁的赖斯的5个孩子中的大部分已经成年，赖斯有了更多闲暇的时间。而因为小儿子爱好科学，赖斯就为他订阅了《科学美国人》。爱好自然科学的她也经常第一时间拿来翻阅，并成了《科学美国人》的著名数学科普作者马丁·加德纳（Martin Gardner）的数学专栏的迷妹。

没想到，那一年的两期《科学美国人》成了赖斯与密铺研究的开端。

1975年7月，加德纳发表了一篇文章（On tessellating the plane with convex polygon tiles），介绍了密铺方面的最新进展。

在了解这些进展之前，我们先来了解一下数学家们在研究密铺的什么性质。

首先，小学生可以很容易理解，任何三角形都可以沿着一边旋转180度，双双配对，然后把整一个平面铺满。再拓展一下，任意四边形，不管是凸的还是凹的，也可以用同样的方式铺满一个平面。

但是，这个结论不能扩展到五边形。比如，正五边形就不行。

那么，是不是任何五边形都不行呢？

1918年，德国数学家卡尔·赖因哈特（Karl Reinhardt）在他的博士毕业论文中证明，有5类五边形可以铺满整个平面。这5类五边形长这样——

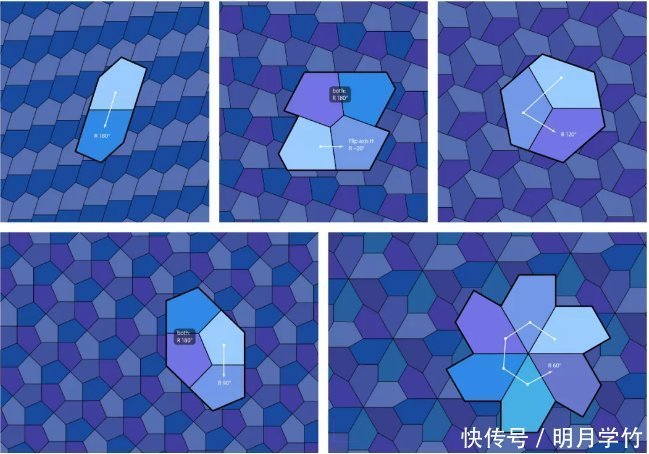
赖因哈特发现的5类可以密铺的凸五边形。（图片来源：Deke McClelland）

赖因哈特发现，只要五边形的边和内角满足一定的条件，就可以铺满一个平面。第1类能密铺的凸五边形很容易理解：只要有任何两条边平行，那么这个五边形就可以密铺。

赖因哈特还指出，凸七边形以及边数超过7的凹多边形无论如何都无法对平面实现密铺。

可是，赖因哈特并不知道自己找到的5类五边形是否完备，也就是说，是否所有能密铺的凸五边形就只有这5类。这个问题也就这样被搁置了50年。

1968年，约翰·霍普金斯大学的数学家理查德·克什纳（Richard Kershner）发现了新的3类凸五边形。这3类五边形要实现密铺，必须要成双成对。

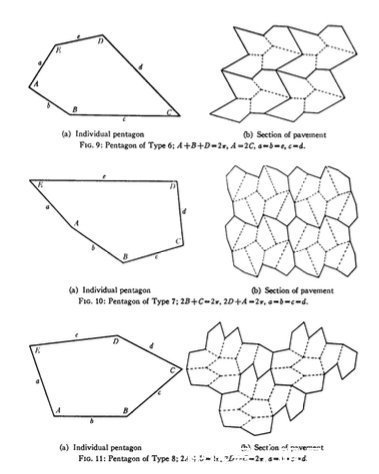
克什纳发现的3类凸五边形密铺。图片来源：（DOI）10.1080/

克什纳认为，能密铺的五边形就这么8类，不能更多了，并在论文中加了一句话：“证明过程太复杂，以后再单独证明”。听起来是不是有费马“对上述命题，我已发现了一种绝妙的证明，可惜书边太窄了写不下。”那味了？

克什纳虽然没有给出完整的证明，但是他的观点却借由 加德纳的专栏被世人所知。

这篇文章刊出后不久，业余数学家理查德·詹姆斯三世（Richard James III）写了一封信给加德纳，告诉他有第9类可以密铺的五边形。

他是从阿基米德地砖（Archimedean tiling）中找到了灵感。实际上，阿基米德地砖中的八边形可以等分为4个五边形。八边形稍微排列一下，就可以在空隙中塞入这种五边形。显然，这种八五边形可以实现密铺。

上一篇：肛肠科女医生3次参加全球数学竞赛，网友评论亮
下一篇：没有了