很多同学常常在数学压轴题型中吃闭门羹，今天就结合这些老师的解法，给大家分享5种解题思路：

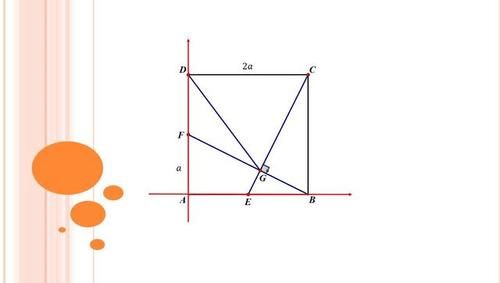
题目：如图1，在正方形ABCD中，点E是AB边上的一个动点（点E与点A，B不重合），连接CE，过点B作BF⊥CE于点G，交AD于点F．

（1）求证：△ABF≌△BCE；

（2）如图2，当点E运动到AB中点时，连接DG，求证：DC＝DG；

方法一：常规的几何思路

过点D做CG的垂线，设AB=2a，在△CBE中利用面积相等，得出BG的长，再证明△CBG≌△DCM，利用全等的性质得到CM的长，最后得出GM=CM，利用垂直平分线的性质可以得到DG=DC。

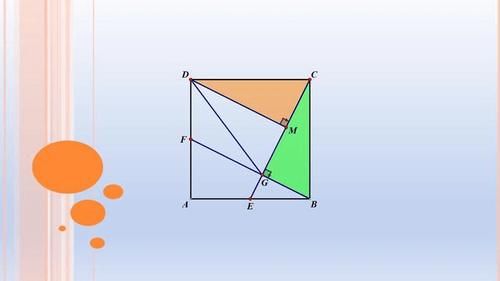
方法二：倍长中线法

我个人认为这个方法是最简单，延长CD，取MD=CD，连接MF，利用△MDF与△BAF相似，可以得到MFG三点共线。因为DG是RT△MGC斜边上的中线，所以DG=DC。

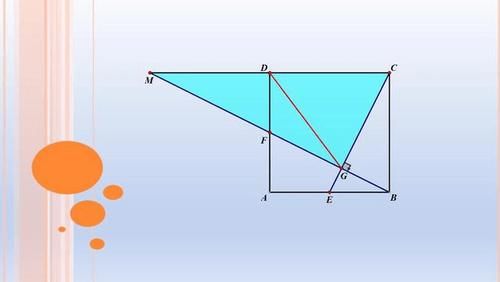
方法三：类似垂直、相等模型

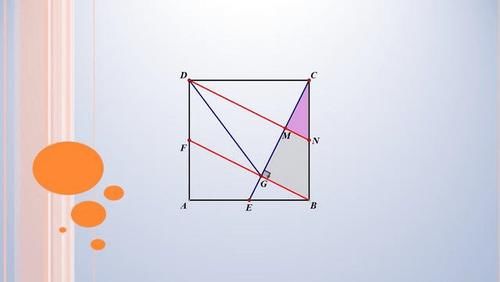
取BC的中点N，因为AD平行于BC，所以∠CMN=90°，易得△CMN相似于△CGB，可证明M为CG中点，于是得到DN垂直平分CG，最后得到DG=DC。

方法四：建立圆的模型

因为∠FDC与∠FGC都是直角，连接FC，所以G、C、D、F四点共圆。因为BC∥AD，所以∠CBG=∠BFA，易得△CDF≌△BFA，得到∠CFD=∠BFA，根据同弧所对的圆周角相等得到∠CFD=∠CGD，再根据同角的余角相等得到∠DCG=∠CBG，所以∠DCG=∠DGC，最后根据相同的角所对的弦相等得到DC=DG。

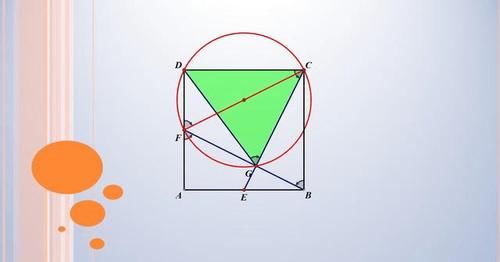
方法四：建立圆的模型

因为∠FDC与∠FGC都是直角，连接FC，所以G、C、D、F四点共圆。因为BC∥AD，所以∠CBG=∠BFA，易得△CDF≌△BFA，得到∠CFD=∠BFA，根据同弧所对的圆周角相等得到∠CFD=∠CGD，再根据同角的余角相等得到∠DCG=∠CBG，所以∠DCG=∠DGC，最后根据相同的角所对的弦相等得到DC=DG。

方法五：建立平面直角坐标系

以点A为原点建立平面直角坐标系，令DC=2a，然后把线段FB、EC的解析式，用含a的式子表示出来，再联立这两个解析式，可以得出点G的坐标，最后求出DG的长，得到DC=DG=2a。

end

点击" 阅读原文 "查看各科知识点汇总